The first idea of neutrino masses, mixing and oscillations was suggested by Bruno Pontecorvo in 1957 [Pon57]. He thought that there was an analogy between leptons and hadrons and that neutrinos could oscillate in an analogous way to the K0-antiK0 system. At that time only one neutrino type was known and the only possible oscillation would be between neutrinos and antineutrinos. After the discovery of the muon-neutrino, it was very natural to Pontecorvo to generalize his first idea to the case of two neutrinos [Pon67]. In this paper, Pontecorvo already anticipated that solar neutrinos could oscillate, before the first Davis’s result. The first phenomenological theory of two-neutrino mixing was soon proposed by V. Gribov and B. Pontecorvo in 1969 [Gri69].
A few years earlier, two-neutrino mixing had been proposed in 1962 by Z. Maki, M. Nakagawa and S. Sakata in a paper which remained unknown for many years [Mak62]. They already assumed that there exists a representation which defines the “true neutrinos” ν1 and ν2 through linear combinations of νe and νμ. The lepton mixing matrix of 3 neutrinos has naturally taken the name PMNS for Pontecorvo, Maki, Nakagawa and Sakata.
The full phenomenological theory of neutrino mixing and the theory of neutrino oscillations in vacuum were developed in the 1970’s. Neutrino oscillation is important by itself, but also because it opens a door towards the mass of the neutrino (neutrino oscillation can happen only if neutrinos are massive), thus towards a modification of the Standard Model of particle physics.
Quantum mechanics allows that the three flavour eigenstates (νe, νμ, ντ) are not necessarily the mass (or propagation) eigenstates but linear combinations of ν1, ν2, ν3, of respective masses m1, m2, m3. There is the relation νl = ΣmUlmνm, where Ulm is the PMNS matrix, which contains three mixing angles θ12, θ23 and θ13:
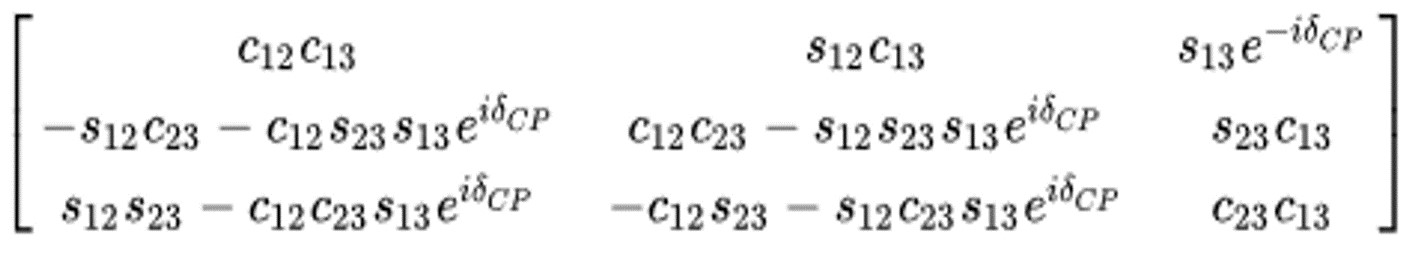
When neutrinos propagate in the vacuum, each mass eigenstate evolves with its own phase factor, which depends on its mass and on its energy. This induces a change of flavor, which has an oscillatory behavior with the distance (hence the name neutrino oscillation). At the detection, the probability P(νi → νj) depends on the three mixing angles and on two Δm2ij (Δm221and Δm223), on the neutrino energy E and on the distance L traveled. To determine the real oscillation parameters θij and Δm2ij, physicists had to play with E and L.
First searches for neutrino oscillations (1980-1990)
In 1980, Reines and collaborators performed a new experiment at the Savannah River nuclear plant. Observing the interactions of antineutrinos on deuterium, they measured the ratio between neutral current and charged current at 11 m from the core of the reactor. The result was 2-3 sigma from the theoretical predictions and has been interpreted as a possible neutrino oscillation [Rei80]. This result has been later proved to be wrong (or overinterpreted), but triggered a lot of experiments to look for neutrino oscillations.
Soon after a French-German-US team searched for neutrino oscillation at the fission reactor of the Laue Langevin Institute (ILL) in Grenoble; they found a result consistent with no-oscillation [Vui82]. The ILL team gave birth to two teams: Goesgen in Switzerland and Bugey in France. In 1984, the two experiments found opposite results: Bugey observed a neutrino deficit interpreted as an oscillation [Cav84] but Goesgen did not confirm. The Bugey team found later the error in the analysis and retracted their premature announcement. There were also several experiments using accelerators at Los Alamos, Brookhaven, Fermilab and CERN [Wot84], all with negative results. In 1998, the Chooz experiment, installing a detector underground at ~1km from the reactor cores, improved the limit on oscillation parameters: excluding neutrino oscillation for sin2(2θ) > 0.18 or Δm2 > 0.9 10-3 eV2 [Apo98,Apo99]. It opened the door to the new generation of detectors (Double Chooz, Daya Bay, RENO) which measured oscillation at about 1 km from the core of the reactors [Abe11b,An12,Ahn12] and made the exact determination of the Θ13 mixing angle.
The MSW effect (1978-1986)
In 1978, Lincoln Wolfenstein showed that the effect of coherent forward scattering must be taken into account when considering the oscillation of neutrinos traveling through matter [Wol78]. Developing this property, Stanislas Mikheyev and Alexei Smirnov showed in 1985 that an adiabatic conversion may be realized if the neutrinos cross matter with slowly varying density: neutrinos may change of flavor in some conditions [Mik85], i.e. electron-neutrinos may transform into muon- or tau-neutrinos. The effect has been named MSW by Albert Messiah at the Moriond Conference in January 1986.
It was soon anticipated, in particular by Bethe [Bet86], that this effect could explain the solar neutrino deficit observed by Davis. Indeed the electron neutrinos produced at the center of the Sun cross all the Sun, whose density varies smoothly by several orders of magnitude until the surface. The idea that electron-neutrinos having disappeared in the Sun could regenerate within some conditions when they reach the matter of the Earth, thus generating the day-night effect, has been then studied [Bou86,Cri86,Bal87].
The oscillation parameters – Towards the PMNS matrix
The many experiments in the 80’s and 90’s did not discover the neutrino oscillation, since the distance and/or the energy did not correspond to the real values of the oscillation parameters.
It happened luckily that, due to the real values of the parameters, the solar neutrino results (transformation of νe into νμ or ντ) have provided information on θ12 and Δm221 and the atmospheric neutrino result (transformation of νμ into ντ) has provided information on θ23 and Δm223. In the solar neutrino sector, the values of the parameters have been mainly determined by the results of SNO [Ahm01,Ahm02] and of the other solar neutrino experiments; they have been further constrained by the results of KamLAND [Egu03], which measured a disappearance of reactor antineutrinos νe from Japan at a mean distance of ~150 km. In the atmospheric neutrino sector, the values of the parameters have been mainly determined by the results of SuperK [Fuk98b]; they have been further constrained by the results of the accelerator experiments K2K, which measured νμ disappearance [Ahn06], MINOS, which measured νμ disappearance and νe appearance using accelerator and atmospheric neutrinos [Ada14] and T2K, which measured νe appearance in a νμ beam [Abe14].
The third mixing angle has been determined since 2012 by the reactor experiments Double Chooz, Daya Bay and RENO [Abe11b,An12,Ahn12], and by the accelerator T2K experiment [Abe11a]. A complete review of the “birth of the PMNS paradigm” is found in [Gig18].

Those values are deduced from the global fit determination of the oscillation parameters (PDG 2022,):

In reality, it is not exact to say that the solution of the solar neutrino problem is the neutrino oscillation. As underlined by Smirnov, it is a combined effect of oscillation and adiabatic flavor conversion of neutrinos in the matter of the Sun via the MSW effect [Smi16].
Further information
A nice account of the history of neutrino oscillation by S. Bilenky can be found in [Bil04].
The online Symmetry Magazine published in February 2010 an article on the discovery of neutrino oscillation.
During the conference on the History of the Neutrino (Sept. 5-7, 2018 in Paris) the subject of Neutrino Oscillation was reviewed by :
- Samoil Bilenky (JINR Dubna, Russia) for the Prehistory of neutrino oscillation emphasing the role of Bruno Pontecorvo : here the slides , the video of his talk and his contribution to the Proceedings.
- Evgeny Akhmedov (MPI Heidelberg, Germany) for the description of the Quantum Mechanics aspects and subtleties of neutrino oscillations: here the slides , the video of his talk and his contribution to the Proceedings.
- Alexei Smirnov (MPI Heidelberg, Germany) for the Mikheyev-Smirnov-Wolfenstein (MSW) effect : here the slides , the video of his talk and his contribution to the Proceedings.
References
| Author(s) | Title | Reference | Key-words | |
|---|---|---|---|---|
| Abe06 | K. Abe at al., Super-Kamiokande collaboration | Measurement of atmospheric neutrino flux consistent with tau neutrino appearance | Phys. Rev. Lett. 97 (2006) 171801; arXiv:hep-ex/0607059 | atmospheric oscillation oscbib |
| Abe11a | K. Abe et al., T2K collaboration | Indication of electron neutrino appearance from an accelerator-produced off-axis muon-neutrino beam | Phys. Rev. Lett. 107 (2011) 041801; arXiv:1106.2822 | historical accelerator oscillation properties milestonebib overviewbib reactorbib oscbib plotbib |
| Abe11b | Y. Abe et al., Double Chooz collaboration | Indication for the disappearance of reactor electron antineutrinos in the Double Chooz experiment | Phys. Rev. Lett. 108 (2012) 131801; arXiv:1112.6353 | historical reactor oscillation properties milestonebib overviewbib reactorbib oscbib plotbib detectorbib |
| Ada14 | P. Adamson et al., MINOS collaboration | Combined analysis of muon-neutrino disappearance and electron-neutrino appearance in MINOS using accelerator and atmospheric neutrinos | Phys. Rev. Lett. 112 (2014) 191801; arXiv:1403.0867 | accelerator atmospheric oscillation oscbib |
| Ahm01 | Q.R. Ahmad et al., SNO collaboration | Measurement of the rate ne + d → p + p + e- interactions produced by 8B solar neutrinos at the Sudbury Neutrino Observatory | Phys. Rev. Lett. 87 (2001) 071301; arXiv:nucl-ex/0106015 | historical solar oscillation msw milestonebib overviewbib solarbib oscbib plotbib |
| Ahm02 | Q.R. Ahmad et al., SNO collaboration | Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory | Phys. Rev. Lett. 89 (2002) 011301; arXiv:nucl-ex/0204008 | historical solar oscillation msw milestonebib overviewbib solarbib oscbib plotbib |
| Ahn06 | M.H. Ahn et al., K2K collaboration | Measurement of the neutrino oscillation by the K2K experiment | Phys. Rev. D74 (2006) 072003; arXiv:hep-ex/0606032 | accelerator atmospheric oscillation oscbib |
| Ahn12 | J.K. Ahn et al., RENO Collaboration | Observation of reactor electron antineutrino disappearance in the RENO experiment | Phys. Rev. Lett. 108 (2012) 191802; arXiv:1204.0626 | historical reactor oscillation properties milestonebib overviewbib oscbib plotbib detectorbib |
| An12 | F.P. An et al., Daya Bay collaboration | Observation of electron-antineutrino disappearance at Daya Bay | Phys. Rev. Lett. 108 (2012) 171803; arXiv:1203.1669 | historical reactor oscillation properties milestonebib overviewbib reactorbib oscbib plotbib detectorbib |
| Apo98 | M. Apollonio et al., Chooz collaboration | Initial results from the Chooz long baseline reactor neutrino oscillation experiment | Phys. Lett. B420 (1998) 397 | oscillation reactor reactorbib oscbib |
| Apo99 | M. Apollonio et al. | Limits on neutrino oscillations from the Chooz experiment | Phys. Lett. B466 (1999) 415 | oscillation reactor reactorbib oscbib detectorbib |
| Ara05b | T. Araki et al., KamLAND collaboration | Measurement of neutrino oscillation with KamLAND: evidence of spectral distortion | Phys. Rev. Lett. 94 (2005) 081801 | reactor oscillation solar overviewbib oscbib plotbib |
| Ash04 | Y. Ashie et al., Super-Kamiokande collaboration | Evidence for an oscillatory signature in atmospheric neutrino oscillations | Phys. Rev. Lett. 93 (2004) 101801 | historical atmospheric milestonebib overviewbib atmosbib oscbib plotbib |
| Bal87 | A.J. Baltz and J. Weneser | Effect of transmission through the Earth on neutrino oscillations | Phys. Rev. D35 (1987) 528 | oscillation msw oscbib |
| Bet86 | H.A. Bethe | Possible explanation of the solar neutrino puzzle | Phys. Rev. Lett. 56 (1986) 1305 | solar msw oscbib |
| Bil04 | S. M. Bilenky | The History of Neutrino Oscillations | arXiv:hep-ph/0410090 | history oscillation oscbib |
| Bou86 | J. Bouchez, M. Cribier, W.Hampel, J. Rich, M. Spiro, D. Vignaud | Matter effects for solar neutrino oscillations | Z. Phys. C32 (1986) 499 | solar msw oscbib |
| Cav84 | J.F. Cavaignac et al. | Indication for neutrino oscillation from a high statistics experiment at the Bugey reactor | Phys. Lett. B148 (1984) 387 | oscillation reactor reactorbib oscbib |
| Cri86 | M. Cribier, W. Hampel, J. Rich and D. Vignaud | MSW regeneration of solar electron-neutrinos in the Earth | Phys. Lett. B182 (1986) 89 | solar msw oscbib |
| Egu03 | K. Eguchi et al. | First results from KamLAND: Evidence for reactor antineutrino disappearance | Phys. Rev. Lett. 90 (2003) 021802 | reactor oscillation solar milestonebib overviewbib oscbib plotbib detectorbib |
| Ell27 | C.D. Ellis and W.A. Wooster | The Average Energy of Disintegration of Radium E | Proc. Roy. Soc. A 117 (1927) 109 | historical betadecay milestonebib overviewbib prehistbib oscbib energybib plotbib |
| Fuk98b | Y. Fukuda et al., Super-Kamiokande collaboration | Evidence for oscillation of atmospheric neutrinos | Phys. Rev. Lett. 81 (1998) 1562 | historical atmospheric milestonebib overviewbib atmosbib oscbib plotbib |
| Gig18 | C. Giganti, S. Lavignac, M. Zito | Neutrino oscillations : the rise of the PMNS paradigm | Prog. in Part. and Nucl. Phys. 98 (2018) 1; arXiv:1710.00715 | review progpn properties oscillation oscbib |
| Gri69 | V. Gribov and B. Pontecorvo | Neutrino astronomy and lepton charge | Phys. Lett. B28 (1969) 493 | historical oscillation theory oscbib |
| Kaj98 | Takaaki Kajita | Atmospheric neutrino results from Super-Kamiokande and Kamiokande - Evidence for muon-neutrino oscillations | Nucl. Phys. B (Proc. Suppl.) 77 (1999) 123 | historical atmospheric milestonebib overviewbib atmosbib oscbib plotbib |
| Lea88 | J.G. Learned, S. Pakvasa and T.J. Weiler | Neutrino Mass and Mixing Implied by Underground Deficit of Low-Energy Muon-neutrino Events | Phys. Lett. B207 (1988) 79 | atmospheric atmosbib oscbib |
| Mak62 | Z. Maki, M. Nakagawa and S. Sakata | Remarks on the Unified Model of Elementary Particles | Progress of Theoretical Physics 28 (1962) 870 | historical oscillation theory milestonebib overviewbib oscbib |
| Mik85 | S.P. Mikheyev and A. Yu. Smirnov | Resonance enhancement of oscillations in matter and solar neutrino spectroscopy | Nuovo Cimento C9 (1986) 17; Sov. J. Nucl. Phys. 42 (1985) 913 (in russian) | oscillation msw milestonebib overviewbib oscbib |
| Pdg22 | R.L. Workman et al., Particle Data Group | The Review of Particle Physics | Prog. Theor. Phys. 2022, 083C01 | review properties oscillation mass propbib oscbib |
| Pon57 | B. Pontecorvo | Inverse beta processes and nonconservation of lepton charge | Soviet Physics JETP 7 (1958) 172 ; ZETF 34 (1957) 247 | historical properties milestonebib overviewbib oscbib |
| Pon67 | B. Pontecorvo | Neutrino experiments and the question of leptonic-charge conservation | Soviet Physics JETP 26 (1968) 984 ; ZETF 53 (1967) 1717 | historical oscillation theory milestonebib overviewbib oscbib theorybib |
| Rei80 | F. Reines, H.W. Sobel, E. Pasierb | Evidence for neutrino instability | Phys. Rev. Lett. 45 (1980) 1307 | oscillation reactor reactorbib oscbib |
| Smi16 | A. Yu. Smirnov | Solar neutrinos: Oscillations or No-oscillations? | arXiv:1609.02386 | solar oscillation msw oscbib |
| Vui82 | J.L. Vuilleumier et al. | New limits on oscillation parameters for electron antineutrinos | Phys. Lett. B114 (1982) 298 - Final results from Gösgen in G. Zacek et al. / Neutrino-oscillation experiments at the Gösgen nuclear power reactor / Phys. Rev. D34 (1986) 2621 | oscillation reactor reactorbib oscbib |
| Wol78 | L. Wolfenstein | Neutrino oscillations in matter | Phys. Rev. D17 (1978) 2369 | historical oscillation msw milestonebib overviewbib oscbib |
| Wot84 | J. Wotschack | Recent results from neutrino oscillation experiments at accelerators | Proc. XI International Conference on Neutrino Physics and Astrophysics - Neutrino 84, World Scientific, p. 117 (first two pages) For the full article (3.4 Mo) | accelerator oscillation oscbib |

Je pinaille encore, mais j’écrirais que KamLAND “measured a disappearance of reactor antineutrinos” plutôt que “of reactor neutrinos”