Neutrino: a fundamental particle of weak interaction
Matter is made of atoms, composed of a nucleus (made of protons and neutrons) surrounded by electrons. Protons and neutrons are each made of three elementary particles named “quarks”. Electrons are one type of elementary particles named “leptons”. According to the standard model of particle physics, there are 6 types of quarks and 6 types of leptons.
The leptons having an electric charge are the electron, the muon and the tau. A lepton with no electric charge is associated to each of them: the electron-neutrino (νe), the muon-neutrino (νμ) and the tau-neutrino (ντ). Within the standard model, the neutrino has a zero mass, a zero charge and a spin ½.
Moreover, the standard model knows only four fundamental interactions between the particles: the strong interaction, the electromagnetic interaction, the weak interaction and the gravitational interaction. Neutrinos can interact only through the weak interaction. It allows them to pass through the Sun or Earth without any deviation or so. This makes their detection very difficult and it requires large masses for the detectors and large neutrino fluxes from the sources.
Parity violation and neutrino helicity

In 1956, T.D. Lee and C.N. Yang (trying to solve the so-called θ-τ puzzle) proposed that parity could not be conserved in the weak interaction [Lee56] and suggested different experiments. This hypothesis has been immediately tested by C.S. Wu and her collaborators (and soon after by others) : by observing an asymmetry of the electrons coming from beta decay of Cobalt-60 nuclei, they proved the non-conservation of parity in weak interaction [Wu57]. To incorporate parity violation in the theory of weak interaction, Lee and Yang (and others) proposed a two-component theory of the neutrino [Lee57] in which the neutrino is left-handed (spin antiparallel to its momentum) and the antineutrino is right-handed (spin parallel to its momentum). This property was called handedness or helicity. Soon after, M. Goldhaber and his collaborators measured the helicity of the neutrino in a beautiful experiment [Gol58]. In addition to those nice results, current (2018) experiments like T2K tend to point also a CP violation in the neutrino sector.
Three families
The Standard Model (which needs to be modified to take into account non-zero neutrino masses) is based on three families of particles, each one associated to one weak interaction flavor. Thanks to the LEP experiments, we know that only 3 neutrino families contribute to the Z width and we suspect that it confirms that only 3 neutrino families are connected to the weak interaction.
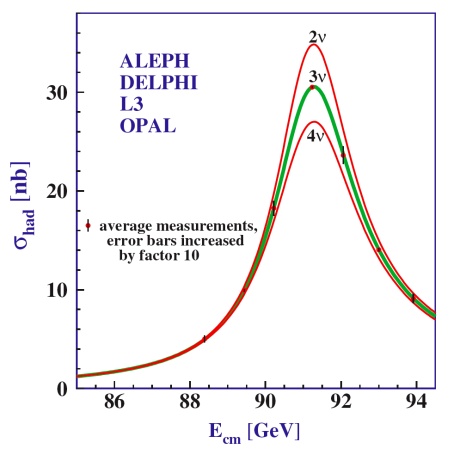
In 1989, the LEP, the new CERN electron-positron collider, designed as a Z factory, started to produce a lot of Z bosons. The study of the width of the mass spectrum of the Z showed that only three light neutrino families exist [Aar89,Akr89,Dec89,Ade90]. This was a major result! Indeed the Z mediates the weak interaction between all fermions and its width increases with the number of families Nν. The combined result of the four LEP experiments (Nν= 3.10 ± 0.10) has been improved and is now Nν= 2.92 ± 0.05, corresponding unambiguously to three light active species [Pdg22] (hypothetic sterile neutrinos would not contribute). The number of neutrinos is also constrained by astrophysical data, by the detection of the neutrino burst from SN1987A and by the cosmological constraint based on the observed He/H abundance ratio in the primordial nucleosynthesis [Den90].
Majorana neutrino
In 1937, Ettore Majorana published a “symmetric theory of the electron and the positron”, in which he hypothesized that particles could be their own antiparticles [Maj37]. This theory was extended immediately to the neutrino by Giulio Racah [Rac37]. Today we know that almost all particles (quarks and leptons) are distinct from their antiparticle: they are said to behave as Dirac particles. “Almost” because we do not know yet if the neutrino is its own antiparticle; in this case it would be a Majorana particle.
The only known method to prove this property is the study of the double beta decay without emission of neutrinos (ββ0ν). A huge experimental effort is in progress which began several decades ago.
Double beta decay
In 1935, Maria Goeppert-Mayer calculated the (very small) probability of simultaneous emission of two electrons and two antineutrinos [Goe35], the double beta decay (2β-decay). This process, rarer than the single beta decay, is characterized by a very large lifetime. In 1939, W. Furry already noticed that there is a marked difference between the results of Majorana’s symmetrical theory of the neutrino [Fur39] and the original Fermi-Dirac theory; in the Majorana theory, only two particles are emitted, two electrons. We still face today the question of the identity of the neutrino (Dirac vs. Majorana) and the search for neutrinoless double-beta decay seems to be the only way to solve this important question.
The first experiment searching for 2β-decay was done by Fireman in 1948 using Geiger counters. In this experiment a half-life limit T1/2>3·1015 years was established for 124Sn [Fir49]. During the period 1948 to 1965 ∼20 experiments were carried out with a sensitivity to the half-life on the level ∼1016−1019 years (see [Hax84]). The 2β-decay was thought to have been ”discovered” a few times, but each time it was not confirmed by new (more sensitive) measurements (in 2011, V. Tretyak published an interesting story of “false starts in history of searches for 2β-decay” [Tre11]); this is true in particular for the geochemical experiment by Inghram and Reynolds in 1950 who studied 2β-decay for the 130Te isotope [Ing50]. It is only in 1968 that the first measurement by Till Kirsten et al. gave a half-life of 1021 years for the 130Te [Kir68].
The direct (and elegant) proof of the double beta decay with neutrinos came in 1987 when Moe and his collaborators observed in a time projection chamber the two electrons coming from the decay of 82Se, energy conservation requiring that two neutrinos were simultaneously emitted [Ell87].
The double beta decay with neutrinos has been observed in about 12 nuclei but the experimental effort since many decades is focused on the search for double-beta decay without neutrinos, which would give the proof that neutrinos are Majorana particles (i.e. their own antiparticle).
Searching for Neutrino Mass
As early as 1933, Francis Perrin showed that the neutrino mass had to be very much lower than the electron mass [Per33]. Once incorporated in the minimal standard model of particle physics, the neutrino had a mass assigned to zero, since there is no right-handed neutrino. This uncomfortable situation did not prevent physicists to build experiments to measure the neutrino mass. Three paths have been used:
- a direct path, based on kinematics of decays;
- a path involving astrophysics (neutrinos from supernovae) and cosmology (study of the cosmic microwave background).
- an indirect path, neutrino oscillation, a mechanism which implies that neutrinos are massive. Neutrino oscillation describes flavor neutrinos (νe, νμ, ντ) as mixtures of neutrino propagation eigenstates with a definite mass (ν1, ν2, ν3).The oscillation mechanism is developed elsewhere and we focus here on the two other paths.
Direct searches
Tritium 3H is radioactive (T1/2=12.3yr) and decays into 3He +e⁻+ νe. It has been considered very early [Kon47] as a good candidate for measuring the neutrino mass, using the kinematics of the decay: by measuring accurately the energy spectrum of the final electron, the region close to the endpoint is directly associated to the mass of the νe (see 2.3 in [Win91]). The first measurements were made in 1949 by Curran et al. [Cur49] and Hanna and Pontecorvo |Han49],using a proportional counter and giving a limit of 10 keV (already 50 times less than the mass of the electron). Using electrostatic and magnetic spectrometers, the limit was improved in 1952, to 250 eV, 2000 times less than the electron mass, convincing most physicists that the mass of the neutrino was identical to zero [Ham53].
Some improvements were made at the beginning of the seventies, in particular by Bergkvist (limit of 60 eV in 1972) [Ber72], until the announcement of a positive result in the spring of 1980. Valentine Lubimov and his colleagues, in Moscow, using a dedicated spectrometer, claimed to have measured a mass of about 30 eV (between 14 and 46 eV) [Lub80]. In 1986, this was contradicted by a team led by Walter Kundig in Zurich and using a similar spectrometer; they found an upper limit of 27 eV [Fri86], later improved to 15 eV. The question “measurement or limit” was open until 1990-1991, when new groups in Los Alamos and Tokyo found upper limits of 9.4 eV and 13 eV respectively (a lively account can be found in p.53-61 of [Sut92]). It was then clear that the Moscow announcement was premature and that the mass of the electron-neutrino was not yet measured and was really very small. In 1999, two new experiments improved the limit to 2.8 eV [Wei99] and 2.5 eV [Lob99]. Today, the first results of the KATRIN experiment [Osi01, Ake19,Ake22] put a the limit at 0.8 eV.
Most of the attempts to measure the neutrino mass focused on the electron-neutrino νe. It is also mandatory to measure the mass of the muon- and tau-neutrinos. Similarly, only upper limits have been obtained, also based on kinematical techniques. The first crude estimate of the muon-neutrino mass, an upper value of ~1 MeV, was given by Barkas in 1956 (before the muon-neutrino discovery!), as a back product of the pion and muon mass measurements [Bar56]. In 1982, the limit obtained studying pion decays in flight, 0.5 MeV, was not significantly improved [And82]. The limit obtained in 1994 by Assamagan et al. (0.17 MeV) has not been improved since more than 20 years [Ass94]. For the tau-neutrino mass, the best limit (18 MeV) has been obtained in 1998 in the ALEPH experiment and is not very constraining [Bar98].
Mass determination from Astrophysics and Cosmology
Astrophysical neutrinos coming from a supernova explosion can also be used to give a limit on the neutrino mass. As soon as 1968, it was anticipated by George Zatsepin that one could obtain an upper limit on the neutrino mass by measuring the difference in the arrival time between low-energy and high energy supernova neutrinos [Zat68]. He also stated that a value of 2 eV (two orders of magnitude lower than the known limit, could be obtained. After the observation of SN 1987A, on February 23, 1987, several authors used the neutrino interactions measured by Kamiokande and IMB to infer a limit on the neutrino mass. For example, Spergel and Bahcall found a limit of 16 eV [Spe88]. The best limit (5.7 eV) has been obtained by Loredo et al. [Lor02] from a detailed and complete analysis.
Assuming big-bang cosmology is correct (today a reasonable assumption), there are also cosmological constraints on the sum of the neutrino masses Σm(νi). The first limit has been obtained in 1966 by Gershtein and Zel’dovich who found 400 eV [Ger66], by considering the gravitational effect of the neutrinos on the dynamics of the expanding universe. In 1972, Cowsik and McClellan made a more detailed calculation (so that the gravitational effect of the neutrino thermal background on the expansion of the Universe be not too severe) and found 66 eV [Cow72] (see also [Sza74]). The interest of these studies has been renewed after the COBE results and the many following developments in cosmology from the 90’s. A first significant limit (2.7 eV) was made by Fukugita et al. in 2000, based on cosmic structure formation in a low-matter density Universe [Fuk00]. Since then, using a lot of new data from the cosmic microwave background, especially from the Planck results, the clustering of galaxies and the Lyman-a forest, the baryon acoustic oscillations and new determinations of the Hubble parameter, the more recent analyses give a limit of 0.15 eV [Pdg22], much smaller than the value obtained from direct measurements.
Coming back to theory, one can say that neutrino masses offer proof of physics beyond the standard model. The Higgs mechanism which provides mass to quarks and charged leptons is not efficient for the neutrinos. The most popular approach (still to be proved experimentally) to give a very tiny mass to the neutrino is the see-saw mechanism which predicts that the product of the neutrino mass by a very large mass (typically the scale of grand unified theories – this mass could be that of a sterile and very heavy right-handed neutrino) is of the order of the square of the typical quark or charged lepton mass [Min77,Gel79,Yan79]. More details can be found in this page.
Further information
During the conference on the History of the Neutrino (Sept. 5-7, 2018 in Paris) the Neutrino Properties were reviewed by :
- Concha Gonzalez-Garcia (U.Barcelona & Stony Brook Univ. Spain/USA) for the global fits establishing the Masses and Mixing of Neutrinos : here the slides , the video of her talk and her contribution to the Proceedings.
- Serguei Petcov (Sissa Trieste, Italy) with Nature of the neutrino (Dirac/Majorana) – Double beta decay with or without neutrinos : here the slides and the video of his talk and his contribution to the Proceedings.
- Francesco Guerra (Sapienza Univ. of Rome, Italy) remind the role of Majorana and neutrinos.: here the slides and the video of his talk and his contribution to the Proceedings.
- and Anatoly A. Smolnikov (MPI Heidelberg, Germany) presented a poster on double beta decay searches with a written contribution to the Proceedings.
References
| Author(s) | Title | Reference | Key-words | |
|---|---|---|---|---|
| Aar89 | P. Aarnio et al., DELPHI Collaboration | Measurement of the mass and the width of the Z particle from multi-hadronic final states produced in e+e- annihilations | Phys. Lett. 231 (1989) 539 | historical numbernu milestonebib overviewbib propbib plotbib |
| Ade90 | L. Adeva et al., L3 Collaboration | Measurement of Z decay to hadrons and precise detemination of the number of neutrino species | Phys. Lett. 237 (1990) 136 | historical numbernu milestonebib overviewbib propbib |
| Ake19 | M. Aker et al. | An improved upper limit on the neutrino mass from a direct kinematic method by KATRIN | arXiv:1909.06048 | propbib properties mass |
| Ake22 | M. Aker et al. (KATRIN collaboration) | Direct neutrino-mass measurement with sub-eV sensibility | Nat. Phys. 18, 160–166 (2022) | propbib properties mass overviewbib |
| Akr89 | M.Z. Akrawy et al., OPAL Collaboration | Measurement of the Z mass and width the OPAL detector at LEP | Phys. Lett. 231 (1989) 530 | historical numbernu milestonebib overviewbib propbib plotbib |
| And82 | H.B. Anderhub et al. | Determination of an upper limit of the mass of the muonic neutrino from the pion decay in flight | Phys. Lett. B114 (1982) 76 | mass propbib |
| Ass94 | K. Assamagan et al. | Measurement of the muon momentum in pion decay at rest using a surface muon beam | Phys. Lett. B335 (1994) 231 - Details in Phys. Rev. D53 (1996) 6065 | mass propbib |
| Bar56 | W.H. Barkas et al. | Mass-ratio method applied to the measurement of the L-meson masses and the energy balance in pion decay | Phys. Rev. 101 (1956) 778 | historical mass propbib |
| Bar98 | R. Barate et al., ALEPH collaboration | An upper limit for the tau-neutrino mass from three- and five-prong tau decays | European Physical Journal C2 (1998) 395 | mass propbib |
| Ber72 | K. Bergkvist | A high-luminosity, high-resolution study of the end-point behaviour of the tritium beta-spectrum | Nucl. Phys. B39 (1972) 317 | mass propbib |
| Blo18 | A. Blondel | The third family of neutrinos | arXiv:1812.11362; Proceedings of the conference "History of the neutrino", 2019 | proceedings conference history propbib plotbib |
| Cow72 | R. Cowsik and J. McClelland | An upper limit on the neutrino rest mass | Phys. Rev. Lett. 29 (1972) 669 | mass propbib |
| Cur49 | S.C. Curran, J. Angus and A.L. Cockroft | The beta spectrum of tritium | Phys. Rev. 76 (1949) 853 | historical betadecay mass propbib |
| Dec89 | D. Decamp et al., ALEPH Collaboration | Determination of the number of light neutrino species | Phys. Lett. 231 (1989) 519 | historical numbernu milestonebib overviewbib propbib plotbib |
| Den90 | D. Denegri, B. Sadoulet, M. Spiro | The number of neutrino species | Rev. Mod. Phys. 62 (1990) 1 | review rmp properties propbib |
| Ell87 | S.R. Elliott, A.A. Hahn and M.K. Moe | Direct evidence for two-neutrino double-beta decay in 82Se | Phys. Rev. Lett. 59 (1987) 2020 | historical doublebeta propbib detectorbib |
| Fir49 | E.L. Fireman | A measurement of the half-life of double-beta decay of Sn124 | Phys. Rev. 75 (1949) 323 | historical doublebeta propbib |
| Fri86 | M. Fritschi et al. | An upper limit for the mass of electron-antineutrino from tritium beta-decay | Phys. Lett. B173 (1986) 485 | mass propbib |
| Fuk00 | M. Fukugita et al. | Limits on neutrino mass from cosmic structure formation | Phys. Rev. Lett. 84 (2000) 1082; arXiv:hep-ph/9908450 | mass cosmological propbib |
| Fur39 | W.H. Furry | On transition probabilities in double-beta disintegration | Phys. Rev. 56 (1939) 1184 | historical doublebeta propbib |
| Gar57 | Richard L. Garwin, Leon M. Lederman and Marcel Weinrich | Observations of the failure of conservation of parity and charge conjugation in meson decays | Phys. Rev. 105 (1957) 1415 | historical properties betadecay milestonebib overviewbib discovbib propbib |
| Gel79 | M. Gell-Mann, P. Ramond and R. Slansky | Complex Spinors and Unified Theories | arXiv:1306.4669Supergravity, ed. by D. Freedman and P. van Nieuwenhuizen, North-Holland (1979) p. 315, retro-print & arXiv:hep-ph/9809459Talk by P. Ramond "The family group and Grand Unified Theories" at the 19th Sanibel Symposium, February 1979, retro-print | historical mass theory milestonebib overviewbib propbib theorybib |
| Ger66 | S.S. Gershtein and Ya. B. Zel’dovich | Rest mass of muonic neutrino and cosmology | JETP Letters 4 (1966) 120 | historical mass cosmological propbib |
| Goe35 | M. Goeppert-Mayer | Double-beta disintegration | Phys. Rev. 48 (1935) 512 | historical doublebeta overviewbib propbib |
| Gol58 | M. Goldhaber, L. Grodzins, A. Sunyar | Helicity of neutrinos | Phys. Rev. 109 (1958) 1015 | historical properties milestonebib overviewbib discovbib propbib theorybib plotbib detectorbib |
| Gro58 | L. Grodzins | Lifetime of a 1- level in 152Sm | Phys. Rev. 109 (1958) 1014 | historical properties discovbib propbib theorybib |
| Ham53 | D.R. Hamilton, W.P. Alford and L. Gross | Upper limits on the neutrino mass from the tritium beta spectrum | Phys. Rev. 92 (1953) 1521 | historical mass propbib |
| Han49 | G.C. Hanna and B. Pontecorvo | The beta spectrum of 3H | Phys. Rev. 75 (1949) 983 | historical betadecay mass propbib |
| Hax84 | W.C. Haxton and G.J. Stephenson | Double beta decay | Prog. in Part. and Nucl. Phys. 12 (1984) 409 | review progpn doublebeta propbib |
| Ing50 | Mark G. Inghram and John H. Reynolds | Double-beta decay of 130Te | Phys. Rev. 78 (1950) 822 | historical doublebeta propbib |
| Kir68 | T. Kirsten et al. | Experimental evidence for the double-beta decay of 130Te | Phys. Rev. Lett. 20 (1968) 1300 | historical doublebeta propbib |
| Kon47 | E.J. Konopinsky | 3H and the mass of the neutrino | Phys. Rev. 72 (1947) 518 | historical properties mass propbib |
| Lan52 | L.M. Langer and R.J.D. Moffat | The beta spectrum of tritium and the mass of the neutrino | Phys. Rev. 88 (1952) 689 | historical betadecay mass propbib |
| Lan57 | L.D. Landau | On the conservation laws for weak interaction | Nucl. Phys. 3 (1957) 127 | historical properties propbib |
| Lee56 | T.D. Lee and C.N. Yang | Question of Parity Conservation in Weak Interactions | Phys. Rev. 104 (1956) 254 | historical properties milestonebib discovbib propbib |
| Lee57 | T.D. Lee and C.N. Yang | Parity non-conservation and a two-component theory of the neutrino | Phys. Rev. 105 (1957) 1671 | historical properties milestonebib overviewbib discovbib propbib |
| Lob99 | V.M. Lobashev et al. | Direct search for mass of neutrino and anomaly in the tritium beta-spectrum | Phys. Lett. B460 (1999) 227 | mass falsepath propbib |
| Lor02 | T.J. Loredo and D.Q. Lamb | Bayesian analysis of neutrinos observed from supernova SN 1987A | Phys. Rev. D65 (2002) 063002 | supernova propbib |
| Lub80 | V.A. Lubimov et al. | An estimate of the electron-neutrino mass from the beta-spectrum of tritium in the valine molecule | Phys. Lett. 94B (1980) 266 | mass falsepath propbib |
| Maj37 | Ettore Majorana | Teoria simmetrica dell’elettrone e del positrone | Nuovo Cimento 14 (1937) 171 | historical properties majorana milestonebib overviewbib propbib |
| Min77 | P. Minkowski | Muon decay into electron and gamma at a rate of one out of 1 billion muon decays | Phys. Lett. B67 (1977) 421 | historical mass theory milestonebib overviewbib propbib theorybib |
| Osi01 | A. Osipowicz et al., KATRIN Collaboration | KATRIN: a next generation tritium beta decay experiment with sub-eV sensitivity for electron neutrino mass | arXiv:hep-ex/0109033 | detection mass propbib |
| Pdg22 | R.L. Workman et al., Particle Data Group | The Review of Particle Physics | Prog. Theor. Phys. 2022, 083C01 | review properties oscillation mass propbib oscbib |
| Per33 | F. Perrin | Possibilité d’émission de particules neutres de masse intrinsèque nulle dans les radioactivités beta | Comptes-Rendus 197 (1933) 1625 | historical properties prehistbib propbib |
| Per34 | F. Perrin | La dissymétrie des spectres beta positifs et négatifs et la masse intrinsèque du neutrino ou ergon | Comptes-Rendus 198 (1934) 2086 | historical properties prehistbib propbib |
| Rac37 | G. Racah | Sulla simmetria tra particelle e antiparticelle | Nuovo Cimento 14 (1937) 322 | historical properties majorana overviewbib propbib |
| Sal57 | A. Salam | On parity conservation and neutrino mass | Nuovo Cimento 5 (1957) 299 | historical properties propbib |
| Spe88 | D.N. Spergel and J.N. Bahcall | The mass of the electron neutrino: Monte-Carlo studies of SN 1987A observations | Phys. Lett. B200 (1988) 366 | mass supernova propbib |
| Sut92 | Christine Sutton | Spaceship Neutrino | Cambridge University Press (1992) | book outreach propbib |
| Sza74 | A.S. Szalay and G. Marx | Limits on the rest masses from big bang cosmology | Acta Physica Academiae Scientiarum Hungaricae 35 (1974) 113 | mass cosmological propbib |
| Wei99 | Ch. Weinheimer et al. | High precision measurement of the tritium beta spectrum near its endpoint and upper limit on the neutrino mass | Phys. Lett. B460 (1999) 219 | mass propbib |
| Win91 | K. Winter ed. | Neutrino Physics | Cambridge University Press, 1991 - 2nd edition 2000 - Contains reprints of several historical papers | book history propbib |
| Wu57 | C.S. Wu, E. Ambler, R.W. Hayward, D.D. Hoppes, R.P. Hudson | Experimental test of parity conservation in beta decay | Phys. Rev. 105 (1957) 1413 | historical properties betadecay milestonebib overviewbib discovbib propbib |
| Yan79 | T. Yanagida | Horizontal symmetry and masses of neutrinos | Prog. of Theor. Phys. 64 (1980) 1103 & "Horizontal gauge symmetry and masses of neutrinos" in Workshop on Unified Theory and Baryon Number in the Universe, February 1979, O. Sawada and A. Sugamoto editors, KEK, Tsukuba (1979) | historical mass theory milestonebib overviewbib propbib |
| Zat68 | G. Zatsepin | Possibility of determining the upper limit of the neutrino mass from the time of flight | JETP Letters 8 (1968) 205 | historical mass propbib |

Je ne voudrais pas pinailler, mais la notion de “three light species” est ambiguë. La largeur invisible du Z ne dit rien sur les neutrinos stériles légers (comme le texte le dit d’ailleurs), contrairement au N_eff de la cosmologie. Il vaudrait mieux parler de “three light active species”, en expliquant ce que cela veut dire.
Je trouve “almost all particles have their own antiparticle” ambigu. Pourquoi ne pas écrire: “almost all particles are distinct from their antiparticle” ?
Je ne dirais pas que la bb0nu est la “only known method” (de prouver que les neutrinos sont des fermions de Majorana), car d’autre processus violant L de deux unités pourraient faire l’affaire, mais c’est la seule méthode qui produise un effet suffisamment grand pour être mesurable en pratique. J’écrirais “The only method that allows to prove this property in practice is the study…”
La terminologie “Fermi-Dirac theory” est-elle standard? Je ne l’ai jamais rencontrée.
Dans les produits de désintégration du tritium, on voit un nu_e (au lieu de l’anti-nu_e).
Ne faudrait-il pas dire qu’en raison du grand mélange leptonique observé, les masses de nu_e, nu_mu et nu_tau ne sont pas bien définies. Il s’agit en réalité de combinaisons différentes des masses des trois états propres de masse.
Pour le seesaw, plutôt que “is equal to the square of the typical quark or charged lepton mass”, je dirais “is of the order of”.